_{Dear
Sir or Madam}

_{I
am writing this letter to you with a request for you to look into a
matter that has to be resolved in physiology as soon as possible. I
would like to invite you to take part in a discussion related to the
theoretical foundations of microcirculation. With my research paper on
these problems, which is now available to you on the Internet, I have
proven
that the hypothesis of the English scientist Starling of 100 years ago
is not only erroneous, but that it substantially hampers the development
of physiology.}

_{In
the past eight years I have worked as an independent researcher. This
type of work leads to many problems, mostly because the state does not
support the research activities of private individuals. Moreover, there
are serious difficulties in practice, connected with the publication of
the research results. All this means great loss of time, especially for
the computer processing of my research. This is why, I am very happy
today about what has been achieved and above all that I can present for
the first time a part of my work in English. Only now I can explain
precisely everything that I wished to write you years ago.}

_{I
hope that you will understand the enormous advantages offered by my
method for solving the problems of microcirculation. The method not only
makes our work easier, but it also broadens our potential as researchers
immensely. If you wish, I can demonstrate this to you personally by
applying my method for calculation of your own research tasks in the
area of physiology in which you
are working.}

_{The
strictly scientific and mathematical approach in my work allows to reach
very categorical conclusions about the present-day situation in the
microcirculation theory. I have worked for many years in the engineering
sciences, in the sphere of hydrology, and subsequently in medicine and
physiology. I assure you that at the moment the development of
physiology essentially needs radical changes. However, their
implementation can occur only by persistently and uncompromisingly going
forward, with correct proof, without assumptions and without hypotheses.}

_{In
my opinion, the biggest problem is to understand that the effective
filtration pressure in the intact tissue does not depend on the
Colloid-Osmotic Pressure (COP). With this I am taking exactly the
opposite stand to that of Starling. The meaning of my theory is
extremely clear, because it consist in the simple discovery that Nature
does not tolerate the wasting of excessive energy in blood circulation
constantly to overcome a factor as COP in the tissue.}

_{The
important thing is that this principle is one of the secrets of Nature,
it has not been invented by me, it exists irrespective of us. I have
discovered it by applying a suitable scientific method for analysis (see
Fig. 2 in my paper).}

_{The
results of my research show that today physiologists have no choice but
to examine the capillaries as elements with distributed parameters. The
capillary is a porous tube and science does not offer another solution
for its fluid dynamics. Today one can no longer work guided by intuition
or by one's senses, when there exists a strictly scientific approach
that invariably leads to the results presented in my work.}

_{In
1896 Starling assumed that COP was the reason for the
refiltration of the fluid filtered in the interstitium. However, he
demonstrated experimentally only that most of the fluid filtered in the
interstitium returns to the capillaries. This achievement has earned him
a permanent place of honour in physiology. However, some of his other
ideas, especially the one about the role of COP in the blood, do not
comply with the theory of fluid dynamics in the blood. And if Starling
were alive today (see Michel, 1997, p. 27), he would probably have been
the first to understand the need to apply the theory about distributed
parameters for calculating the fluid volume in the tissue. And this
theory is more convenient and more understandable than all earlier
hypotheses in the sphere of microcirculation.}

_{More
than 100 years later, the time has come to change the theoretical
foundation of microcirculation, which means that it is necessary to
create absolutely new concepts in physiology. In this sense, I am
addressing this letter as an appeal not only to physiologists throughout
the world, but also to all researches who have an opinion on these
matters.}

_{This
is an appeal to you personally to choose your position in an inevitable
dispute, which will have to decide the future of the theory of
microcirculation. There is no time to postpone this problem further,
because we all share a responsibility for physiology, science in general
and the future generations.}

_{With
the present contribution to the theory of microcirculation, today I am
giving the start of an extremely needed updating of physiology. There is
still a lot to be done in the future and it can be done only with the
united efforts of all of us. Not only physiology, but the science about
living nature in general, compels us to do our job well. Therefore, I
shall be happy to learn that you would be among the first who would
understand me and support me.}

_{There
is no doubt that it would become necessary for physiologists to work
with scientists from domains outside physiology, with mathematicians,
physicists, biologists, systems theoreticians, theoreticians in the
field of hydrology, etc. Within the frameworks of such interdisciplinary
groups on problems related to tissue supply it would be possible to
demonstrate best and most quickly the correctness of my conclusions.}

_{Today
I am requesting concrete assistance. If you think that it would be a
good idea to invite me for a discussion or for joint work, I am entirely
at your disposal. Besides, you can invite me to publish my papers in
your journal/specialized publication. For a year my work can be found in
the State Library of Bavaria and on the Internet: http:\\www.jmpetrow.de}

_{Looking
forward to hearing from you, I thank you in advance and remain with best
wishes,}

_{Yours
sincerely,}

_{Jordan
M. Petrow}

_{Personal
information:}

_{I
have doctorates in medicine and systems theory, was educated in
physiology at the University of Rostock and acquired the title of "specialist
in physiology". I currently work as a doctor in Bad Tölz: Dr.Dr.
Jordan M. Petrow, Badstraße 26, 83646 Bad Tölz, Germany, Tel. 0049
8041 799755, E-Mail: petrow@t_online.de}

_{100 Years since Starling's Hypothesis in Physiology:
100 years along the path of a Misunderstanding. Response to C. C.
Michel's Laudation on the Occasion of the Centenary}

_{Jordan M. Petrow}

_Contents:

_Abstract

_Introduction

_{Theory
of the fluid dynamics of a porous tube, like the capillary, in a limited
and elastic space, like the cellular interstitium}

_{Basic
rules}

_{Basic
mathematical rules}

_{Discussion
1: The opportunities of the new theory of microcirculation}

_{Discussion
2: New interpretation of the isogravimetric method}

_{Discussion 3. The errors in Starling's hypothesis and
in the current microcirculation theory}

_References

_{Key words:}_{Microcirculation in tissues, Starling’s hypothesis,
blood pressure, oncotic pressure, interstitial hydraulic pressure, lymph
formation, filtration, fluid exchange, capillary filtration coefficient.}

_Abstract

_{The present-day theory of microcirculation, based
above all on the hypothesis of the British scientist Starling of 100
years ago, treats blood pressure and colloid-osmotic pressure (COP) as
opposing forces in the process of tissue perfusion. According to this
theory, the blood pressure increases the convective fluid flux through
the cellular interstitium, while COP reduced this flux. Since this
concerns the nutritive supply of the tissue with essential
life-supporting substances, a model like Starling's hypothesis does not
seem appropriate for satisfying the extremely strict criteria in the
evolutionary course of Nature.}

_{Just the
opposite to the statements in Starling's hypothesis is proven in the
present work, namely that the blood pressure and COP are mutually
complementary in the process of supplying the tissue. COP not only makes
respiration possible, as the basis for the emergence of life on land,
but it normally doubles the potential for intensification of the tissue
perfusion. The value of the effective filtration pressure (EFP) in the
intact tissue is not reduced parallel with the COP value, as was
believed in physiology until now, because under real conditions and in
the absence of transient processes, EFP to the capillary wall is
determined above all by the blood pressure and does not depend on COP.}

_{When Starling
formulated his hypothesis in 1896, he expressed an assumption about the
fluid exchange on the capillary wall. However, 100 years after Starling,
it is no longer necessary to restrict ourselves within intuitive notions
only.}

_{Unlike
Starling, in the present work the solution to the problem is achieved
through correct mathematical means, on the basis of the experience
accumulated both in physiology and in the systems theory. Since the
capillary and the tissues around it are specific elements with
distributed parameters, special mathematical methods are needed to solve
the problems formulated. From a scientific point of view, the analysis
demonstrated in the present work are absolutely mandatory for the
microcirculation theory.}

_{1.
Introduction}

_{The mechanism
of supplying oxygen and other vitally essential substances to the cells
of the living organism is an integral part of the eternal question
related to the emergence of life on Earth, because every more complex
form in the animal world does exist only by a blood and blood
circulation system. And it is not accidental that this system has become
identified in our conscience with a symbol of vitality, because the
quality of supplying the cells defines above all the surviving of every
organism, limits its possibilities for action and simply solves the
problem: to live or to die.}

_{In medicine,
the problems related to the supplying of the cells in tissues are
referred to the domain of microcirculation. This is an independent
scientific area, which is predominantly within the scope of interest of
physiologists.}

_{The known
hypothesis of the great British scientist Starling gained prominence in
the past 100 years for explaining the problems of microcirculation in
physiology. Starling discovered 100 years ago that most of the fluid
filtered in the cellular interstitium returns to the capillaries. In
this way, he revised other hypotheses of that time and thus he reserved
a permanent place of honour for himself in physiology. This fact is
particularly well highlighted in C.C. Michel's comprehensive work
(1997), marking the centenary of Starling's hypothesis (p. 27):}

_{"I
am sure that if Starling were alive today he would be happy to know that
his hypothesis had been so fruitful in clarifying thinking and
encouraging experimentation."}

_{Starling assumed that the colloid-osmotic pressure (COP)
in the blood causes the moving of a part of the interstitial fluid back
to the capillaries through reabsorption. The microcirculation theory in
our time has accepted this statement by Starling and also presents COP
as a force acting directly in the opposite direction to the blood
pressure. Otherwise the blood pressure determines the paracapillary
interstitial flux (flow), being the most important carrier of oxygen and
of other vital substances necessary to the organism. If we assume
Starling's claim about COP to be true, we would also have to agree that
a benefit to evolution of the type of COP had been irrationally created
to oppose the most vital of all life-determining factors. So far no one
has thought about the problem that such a questionable "benefit”
would inevitably lead to additional energy expenditure in the
cardiovascular system. The
main task of this system is to supply the cells of the organism, and
precisely during this task approximately a quarter of the cardiac power
ought to be wasted in the capillary bed for overcoming a relatively
constant value, such as the resultant COP.
And when it comes to the energy balance in the
organism, Nature never tolerates spokes to be put in the wheel of
evolution. Therefore, from a purely pragmatic point of view, Starling's
idea appears to be extremely inexpedient, even at first glance.}

_{Starling
reached his conclusions 100 years ago as a result of the experimental
observation that the volume of a tissue starts decreasing when COP in
the blood increases, and conversely, that same volume starts growing
when the blood pressure increases. This antagonistic effect of the two
parameters is so blatantly obvious that it later served as the basis for
devising the so-called isogravimetric method for practical research.
Using this method, the dependence is sought between the different values
of the blood pressure and COP, while at the same time making sure that
the volume or the weight of the tissues studied remain constant
(Pappenheimer, J.R. and A. Soto-Rivera, 1948).}

_{The convenience
of this isogravimetric method consists in the fact that the values
studied can be measured outside the tissue, because very soon there
appeared a growing awareness in modern physiology as well that
researchers would face insurmountable difficulties trying to conduct
similar measurements within the tissues and at cellular level. However,
experience was accumulated in physiology over the years and already
after Starling's death a mathematical expression of his hypothesis was
obtained, which can be seen for the first time in the publications of
Landis of 1927 (see also Michel, 1997):}

_J_{v/A = Lp
[(Pc-Pi)
- (}_p_{c -}_p_{i
)] = Lp (D}_{P -}_D_p_{),
(1)}

_{where Jv/A
is the fluid rate per unit area of capillary wall. Pc and}_p_{c are
respectively the capillary pressure and oncotic pressure of the blood; Lp
is the hydraulic permeability of the capillary wall and Pi and}_p_{i are
respectively the hydraulic pressure and oncotic pressure of the
interstitial fluid.}

_{Other
modifications of equation (1) appeared later, but they do not change
essentially the basic construction of Landis:}

_J_{v/A
= Lp [(Pc-Pi)
- S
sr
D}_p_{r
],




                (2)}

_{r =1}

_{where
sr
is the osmotic reflection coefficient of the microvascular wall to the
r-th solute. D}_p_{r
= (}_p_{c
-}_p_{i
) is the difference in the oncotic pressures of the r-th solution
flanking the capillary membrane.}

_{To
interpret equation (1) means first of all to draw the conclusion that
COP represents energy loss of the cardiac activity in the capillary bed.
The second interpretation of equation (1) is that the antagonism between
the blood pressure and the resultant COP
= D}_p_{r
= (}_p_{c
-}_p_{i
) occurs at the level of the capillary wall. This
conclusion will be explained in greater detail in the next section.}

_{Bearing in mind that COP has a relatively constant
value within the capillaries and that the blood pressure along the
capillary length decreases progressively, it is also possible to
construct a graphic image of Starling's hypothesis, as shown on Fig. 1.
This is a graph that can be seen in any physiology book.}

_{In addition to
the already cited energy wasting in the capillary bed, the theoretical
concept presented on Fig. 1 contains a range of other shortcomings,
which will be only briefly mentioned here:}

_1. _{In constructing the graph on Fig. 1,
it is assumed without any evidence that the interstitial hydraulic
pressure (IHP) is also a constant value. However, how are the values of
the hydraulic pressure assumed to remain constant behind a porous wall,
when before that same porous wall the values of the hydraulic pressure
are to be changed, see also Discussion 3, items 13-19.}

_2. _{According to the concept in Fig. 1,
the system is incapable of meeting even the most elementary stability
criteria. The area of its reliability is actually infinitely small and
this conclusion does not correlate in any case with the practical
observations in living nature.}

_3. _{If the values of the blood pressure
and the resultant COP are nearly equal, the interstitial fluid flow
ought to be stopped. What is the meaning of this conclusion, if there
are cells behind the capillary wall, for which this interstitial fluid
flow is vitally essential?}

_4. _{If the resultant COP is increased
substantially, the interstitium should become dry. This is not observed
in practice and the question about the nature of the force which is
opposed and which in the long run neutralizes the action of COP remains.}

_5. _{From a mathematical point of view,
it is not possible to operate with a conception similar to
equation (1), because it requires the practically impossible condition
to measure the values concerned in each point along the capillary wall.
Therefore, this concept does not allow to calculate the different
parameters in time and in other dimensions, in the beginning of a
process (t®0)
and at its end (t®¥).}

_{Each of the
shortcomings listed above is in itself sufficient for rejecting
Starling's hypothesis as inconsistent. However, item 5 expresses the
real problem of physiology, from its inception as a science to this day:
So far there is no suitable method in the microcirculation theory for
calculating the fluid exchange on the capillary wall.}

_{2.0.
Theory of the fluid dynamics of a porous tube, like the capillary, in a
limited and elastic space, like the cellular interstitium}

_{2.1.
Basic rules}

_{We
shall divide the theory of porous tubes into two parts. In this Section
2.1 it will be explained descriptively, which will make it easier to
understand its meaning and its philosophy. This will be a preparation
for Section 2.2, where a mathematical calculation only will be presented.}

_{Creating
a theory about the tissue supply necessitates first to have some idea
about the structure of the tissues. And if we are talking about fluid
dynamics, it is necessary to know what there is behind the capillary
wall and above all how the interstitial space ends.}

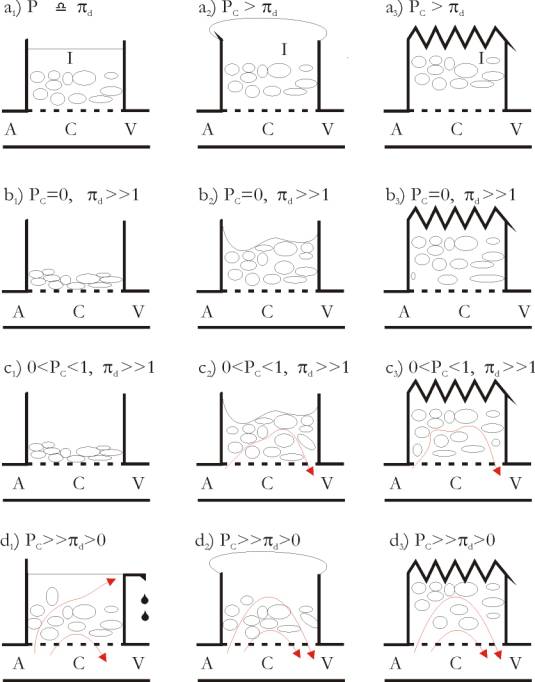
_{In
principle, there are four possibilities, the first of them being that
the interstitial space is simply open (Fig. 2a1). Although ostensibly
absurd, such a situation cannot be totally ruled out in Nature, e.g., in
fish gills. The second possibility is the interstitial space to be
closed by a membrane, which is both elastic and very soft (Fig. 2a2).
The third possibility is the interstitial space to be closed by a
membrane, which is elastic and sufficiently strong, so that together
with the cells it can resist some maximum interstitial hydraulic
pressure, e.g., about 200-300 mm Hg (Fig. 2a3). The fourth possibility
derives from the third one, if the interstitial membrane is supported
mechanically by some bone structure. Such is the situation, for example,
in the cranial cavity, but this situation will not be considered here,
because it can easily be reproduced from Fig. 2a3. Therefore, it is only
necessary to make the provision that the elasticity of the interstitial
membrane tends to zero.}

_{The
second step along the way to creating a theory on tissue supply is to
find an explanation of the antagonism observed in practice between the
blood pressure and COP. So far no one in physiology has made the
distinction that:}

_1. _{The antagonism between the blood
pressure and COP may occur in principle at the level of the capillary
wall. However, we shall prove below that this condition is fulfilled
only when the tissue interstitium is open. An open interstitium is not a
normal phenomenon in Nature, it exists only in the respiratory organs of
sea animals (e.g. fish gills). For all other cases of life,}

_2. _{The antagonism between the blood
pressure and COP occurs in the tissue at the level of the interstitium,
more specifically at the level of the interstitial pressure IHP. This
occurs always and for all cases of intact tissue with closed
interstitium. This closed interstitium resembles in its most elementary
form the construction of a natural osmometer, which consists of a
semi-permeable membrane placed in a liquid medium and in a closed space.}

_{The closed interstitium of tissues is the normal
state for all living creature on Earth. However, the theory which we are
proposing in this chapter and in the next is equally valid both for open
and for closed interstitial spaces:}

_{The third step along the way of creating a theory
is to accept at first equation (1) and to find the respective situation
among the four types of tissue realization, which corresponds to this
equation. If along the capillary on Fig. 2a1, the hydraulic
pressure on both sides of the capillary wall is measured in many
different points, it will show that this gives validity to equation (1).
However, the graphic expression of the values measured will not
correspond to Fig. 1, but it will fit very well Fig. 5c, which is
already calculated according to the new microcirculation theory.
Moreover, the experiment will show that equation (1) is valid for the
situation on Fig. 2a2 as well.}

_{The
construction from Fig. 2a1 can easily be reproduced experimentally and
it can even be built using suitable artificial materials. However, no
such case exists in living Nature on land. Contrary to this, the
situation in Fig. 2a2 can be realized as an experiment with a living
tissue, while all of the tissue structures are still completely
preserved. Thus, it becomes clear how close it is to assume that the
dependence found here (Fig. 2a2) in the form of equation (1) will also
be valid for all other situations in Fig. 2. Starling himself conducted
his experiments mainly with cell tissues in oedematous state, as in Fig.
2a2. This is probably why he wrote in 1896:}

_{“…
and whereas capillary pressure determines transudation, the osmotic
pressures of the proteins of the serum determines absorption. Moreover,
if we leave the frictional resistance of the capillary wall to the
passage of fluid through it out of account, the osmotic attraction of
the serum for the extravascular fluid will be proportional to the force
expended in the production of this latter, so that, at any given time,
there must be a balance between the hydrostatic pressure of the blood in
the capillaries and the osmotic attraction of the blood for the
surrounding fluids (E.H. Starling, 1896)...“}

_{From
this quotation it becomes clear that here COP and the blood pressure are
considered as two opposing forces. This is actually the fundamental idea
defining Starling's hypothesis, equation (1) and the present-day theory
of microcirculation. As we indicated already, this idea
is true for Fig. 2a1, because there the capillary wall represents a kind
of boundary behind which an interstitium with infinite compliance starts.
In this case, for the antagonism between the blood pressure and COP
there is no other choice but to exist at the level of that capillary
wall. In this way, the capillary wall on Fig. 2a1 is the substrate basis
for the validity of equation (1).}

_{However,
what is true of the tissue from column 1 cannot in all cases be applied
to explaine the situations of the second and third columns of Fig. 2.
Here it is not possible for a science to be objective and not to notice
that column 1 differs radically from columns 2 and 3, and that this
difference is due above all to the membrane closing the interstitium.
Practical measurements as those in Fig. 2a1 cannot help in the concrete
case, because they inevitably lead to destruction of the membrane
closing the interstitium and to creating conditions that are valid for
column 1. Therefore, the conditions of columns 2 and 3 on Fig. 2
necessitate another type of analysis, which will be described below:}

_{With
the values given in Fig. 2b, it is logical to conclude that the soft
tissue oedema from Fig. 2a2 will already be resorbed as a result of the
suction effect of COP, whereby the membrane serving as a sheath of the
cellular tissue would move towards the cells and would stop after a
certain time, because the cellular bodies would prevent it from
approaching closer to the capillary wall. When the movement of this
membrane stops, the suction force of COP will cause a subatmospheric
(negative) hydraulic pressure in the interstitium. Actually, this is
precisely the principle of operation of the devices for COP measurements.
In this way, a complete equilibrium of the forces is reached in the
situation on Fig. 2b2, whereby COP suction force is neutralized by the
resistance of the soft membrane covering the cells and is supported by
the cell bodies. In this system there are no longer movements either of
the membrane, or of the fluid that is still present between the cells in
the interstitium. These are the main postulates of Fig. 2b2, which
constitute a radical difference from the situation in Fig. 2b1 with an
already dry interstitium.}

_{At
this point it is necessary to understand that in the steady state of
forces on Fig. 2b2, any increase in the blood pressure D}_P_{c,
= PCA – PCE, even infinitely small, would result in the
system being taken out of its steady state. PCA and PCE are respectively
the blood pressure at the entrance and the blood pressure at the end of
the capillary.}

_{As
shown on Fig. 2c2, this very small increase in D}_P_{c
will immediately cause a convective flow}_J_{vi
=
D}_P_{c/Ri
of the interstitial fluid through the interstitial space (i =
interstitial, pressure/resistance relation according to Ohm`s Law).
Cave: There will be no such convective flow in the situation
shown on Fig. 2c1 and there the interstitium will continue to be dry.
On the other hand, the processes in Figs. 2b3 and 2c3, respectively will
be analog to Figs. 2b2 and 2c2.}

_{There
is no doubt that whoever has understood the essential difference between
the first and the second columns of Fig. 2 would also understand the
basic postulates of the new theory on microcirculation. It should simply
be known that the blood pressure even in an interstitium with
subatmospheric interstitial hydraulic pressure (IHP) will cause a
convective flow, because there is no force that can oppose it, as in the
described case the COP force is already completely neutralized with the
help of the mechanical support of the tissue membrane. Moreover, in this
case it does not matter in the least whether the tissue membrane is very
soft, both elastic and soft, elastic and sufficiently strong, or totally
rigid, as in a bone cavity. It can be pointed out as an extreme example
that in the lungs the role of such a sheath (membrane) is played by the
surface tension of the alveolar fluid.}

_{The
fourth line on Fig. 2 shows the different responses of the three types
of cell tissue to the condition of forced perfusion. In Nature this
condition is imposed with every physical loading of the organism.
Interstitial fluid flows from the tissue in Fig. 2d1, a pathological
oedema develops in Fig. 2d2, and only in Fig. 2d3 the paracapillary flow
through the interstitium can be increased many times, as required by the
condition for forced perfusion. The examples show that situations as
those in Fig. 2d1 cannot exist in the organism, situations as those in
Fig. 2d2 should not exist, whereas in the situations in Fig. 2d3 the
tissue should possess sufficient internal bonds so as to withstand the
loading.}

_{The
mechanism of COP neutralization in a closed interstitial space is the
most important characteristic feature of the porous capillary. However,
this condition is not always completely fulfilled in some capillary
constructions. The specificities of the renal glomerules can be cited as
an example. This is why, Fig.3 presents more precisely the mechanism of
COP neutralization. In a porous tubing placed under suitable conditions,
the COP force at the beginning of the tubing is neutralized by the COP
force at the end of the tubing, i.e., COP neutralizes COP. In this
brilliant construction of Nature, the liquid medium in the interstitium
is the link between the opposed COP forces. It is understood now that
the tissue sheath (membrane) plays a secondary role in this process, but
without it there can be no effect of COP neutralization, because in that
case the interstitial space obtains an
infinite compliance and thus the interstitial fluid cannot function as a
link.}

_{The mechanism
for compensation of the COP force means that the blood pressure in a
tissue system with COP filters in the same way in the direction of the
interstitium as in a tissue system without COP. There is no force
opposing the blood pressure in an intact tissue in a steady state. This
means that equation (1) is wrong and 100 years after Starling we can
write:}

_{The
first property of the theory of porous tubings, such as the
capillaries, placed in a closed space with finite dimensions, such as
the cellular interstitium, is the fact that the paracapillary
interstitial flow in a steady state is determined only by the blood
pressure and does not depend on the resultant COP, acting along the
capillary wall.}

_{In
a steady state and with a constant volume of the intact tissue, the
suction force of the resultant COP in the capillaries is projected in
the interstitium and lowers the interstitial hydraulic pressure IHP.}

_{The
second property of the theory of porous tubings, such as the
capillaries, placed in a closed space with finite dimensions, such as
the cellular interstitium, is the corollary that the interstitial
pressure IHP in intact tissues decreases with the value of the
resultant COP, acting along the capillary wall.}

_{In
the next section these two properties will be derived mathematically.}

_2.2. _{Basic mathematical rules}

_{The capillary
is a porous tubing placed in the interstitial space with defined elastic
properties. It is completely futile to make attempts to calculate such
structures using equation (1), because they are systems with distributed
parameters. This definition comes from the scientific domain of the
systems theory. Another example of such systems is a telephone circuit
over a distance of thousands of miles. Here it is important that the
systems with distributed parameters are calculated using special
mathematical methods. This is why, the capillary cannot be considered as
an ordinary tube, although it does not exceed 1 mm in length. This small
tubing is porous and the millions of pores along the capillary length
make all parameter values dependent on the place where they are acting.
This peculiarity necessitates to treat the capillary as a sum of
numerous separate segments, infinitely small in themselves, or at least
small enough to the extent of ruling out the already cited distribution
of the parameters for the individual segment. This condition leads to a
substitutive diagram of the capillary, and this rule is also valid of
the cases when numerous capillaries share one interstitial space and
form a so-called substituting capillary in a certain part of the cell
tissue.}

_{In
order to construct the substituting diagram of a capillary, it is
necessary to know above all how to express the different properties of
the tissue elements taking part in the microcirculation. For this
purpose, there is a scientific domain dealing with the so-called
electromechanical analogies. The aim here is to create a common
scientific base by means of which certain principles in, e.g., hydrology,
may already be expressed through familiar electromechanical concepts. We
have used the following parameters for the construction of the
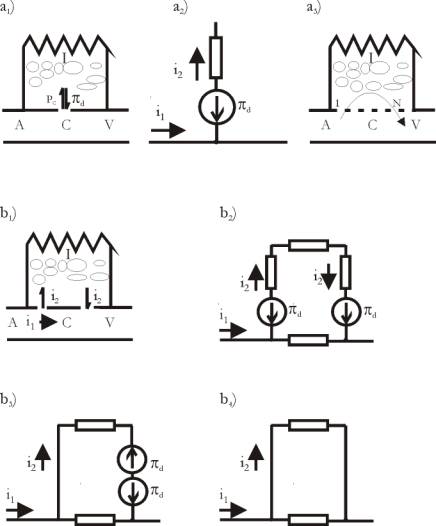
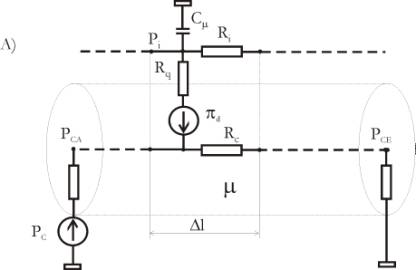
substituting diagram of the capillary, according to Fig. 4a:}

_· _{The hydraulic resistance inside and
along the capillary}_{. Every capillary segment
with elementary length D}_l_{opposes the blood flow with a resistance which we have designated with Rcm.
Here m
is an index of 1 – N, where N is the total number of the capillary
segments.}

_· _{Capillary filtration coefficient.}_{This
coefficient determines the permeability of the capillary wall for the
indicated segment. It is replaced by a resistance Rqm
in each segment and is placed transversely to the capillary wall.}

_· _{The hydraulic resistance of the
interstitial space.}_{Each tissue is characterized
by its own structure of its interstitial space, which opposes the
paracapillary fluid flow with a definite resistance. It may also change
for the different segments, hence it also receives an index and is
designated with Rim.}

_· _{COP on the capillary wall.}_{The action of COP here is suction depending on the direction of the
colloid-osmotic gradient. This property is accepted in full
correspondence to all earlier observations of experimental physiology.
Similar to the blood pressure, COP is a vector force}_p_{d,
which is designated as an arrow in a circle and receives a separate
index m
for each segment.}

_· _{Hydraulic capacity C}_m_._{This value expresses the capacity of the
interstitial space to incorporate fluids and characterizes the elastic
properties of the interstitial structures.}

_{By
means of the listed structures it is possible to obtain the substituting
diagram of the capillary, which is shown on Figs. 4a and 4b. Actually,
the construction on Fig. 4b is the most important stride forward,
because after it the calculation of the separate parameters becomes a
purely technical problem. For example, the elementary flux Jvm
in the respective segment can be found according to the following
formula:}

_J_{vm
= mm
. PCA + S
njm
.}_p_{dj,


                (3)}

_j=1

_{where
PCA is the blood pressure at the beginning of the capillary, m
and n being coefficients with conductivity dimension.}_p_{dj
is the resultant COP for the respective segment, N denotes the total
number of capillary segments.}

_{The
effective filtration pressure EFP at the capillary wall is defined as a
pressure decline against the respective resistance Rqm.
If this resistance along the capillary remains constant, the graphic
image of EFP coincides in principle with that of Jvm
by using another dimension.}

_{EFP
= Jvm
. Rqm


    (4)}

_{The
blood pressure Pcm
along the capillary can also be calculated according to the diagram on
Fig. 4b, but for the sake of brevity, we cannot discuss all parameters
here. However, the complete calculation of the substituting diagram is
much simpler than one can think after the first impression of equation
(3). Computer programmes for this purpose have existed for a long time
and they offer the biggest details in a ready form.}

_{In
this way, the calculation even of the most complicated situation
in the sphere of tissue perfusion is reduced to a single click with
the computer mouse. Naturally, this is an enormous relief for the
researchers of microcirculation, who will be expected in the future
only to learn to cope with concepts of electromechanical analogies, in
order to be able to construct the substituting diagrams of the objects
studied. In this way, microcirculation will thus at long last acquire
the advantages that have entered other research branches of science a
long time ago.}

3.1. Discussion 1: The opportunities of the new theory of microcirculation

_{So
far we presented the theory of fluid dynamics in porous tubing, like the
capillaries, when they are in a closed space, like the tissue
interstitium. The calculation of the substituting diagram of the
capillary produced the same results, which we obtained descriptively in
section 2.1. There is no point in doubting the actual calculation,
because it is merely a mathematical inventory that has been accepted in
science for a long time. Therefore, here we are restricting our
discussion only to the type of the substituting diagram of the
capillaries.}

_1. _{The description of the capillary in
accordance with Fig. 4b is the only correct way to derive the
microcirculation theory. There are no other possibilities in science for
calculating elements with distributed parameters. Naturally, the
description on Fig. 4b is after all only a model of blood supplying the
tissues. However, real science exists only in accordance with a model.
Merely verbal notions are not in the least sufficient, because even the
simplest practical measurement requires the respective scientific model,
according to which the interpretation of the measured value should be
made.}

_2. _{Starling's hypothesis is in itself
also a model. The expression from Starling's quotation “... Moreover,
if we leave the frictional resistance of the capillary wall to the
passage of fluid through it out of account...” (see 2.1), means, for
instance, that Starling is proposing here a simplification. However, he
could not provide any justification for this simplification, because he
lacked the respective mathematical model. However, we specifically
indicate on Fig. 4a that Starling referred to the resistance Rqm.
Moreover, we can prove that according to the new theory, this resistance
plays a role mainly in transient processes by determining their duration.
Therefore, in some special cases considered, the resistance Rqm
can indeed be ignored. However, such a simplification is not done
intuitively, it should obligatorily be scientifically substantiated, see
also item 6 below.}

_3. _{The description on Fig. 4b is
universal, because it can be used to calculate capillaries from all
kinds of tissues. This
method allows us to study the fluid exchange both in inhomogeneous
structures and in non-linear processes in the tissues. In addition, the
model in Fig. 4b can be infinitely enlarged, e.g., for increasing the
precision or for examining lymph processes. In the concrete case, a
homogeneously structured capillary is presented on Fig. 4b, because this
model is perfectly sufficient for measuring the essential dependences
between the values determining the fluid exchange on the capillary wall.}

_4. _{The new theory permits studies of
the parameters depending on time, which means that for the first time it
can also be used to account for the transient processes in
microcirculation (Fig. 6). On the other hand, this possibility allows to
use certain test functions (Fig. 6c), as this is done in the systems
theory. On the basis of the information obtained with the test functions
it is possible to determine the unknown values in microcirculation,
which cannot be measured directly for one reason or another.}

_5. _{It should be borne in mind that in a
steady state the action of the elastic elements in the tissue, and hence
the influence of time, no longer exist, compare with Figs. 6d, 6f, 6g.
In this case the interstitium of the tissue is treated as an inelastic
and closed compartment with a constant volume.}

_6. _{One of the most important properties
of the theory of porous tubes, like the capillaries, can be seen by
comparing the figures 6b and 6d. From the comparison it becomes clear
that the quality of the process is invariant with respect to the value
of its parameters. In other words, it is shown here that the law binding
the elementary values R and C does not depend on the
concrete relations between these two values, because whatever values are
used to substitute the values R and C, the process remains
unchanged in principle. Only the amplitude and the scale in time change
on Figs. 6b and 6d.}

_{At
this point it is possible to see the advantage of the new
microcirculation theory over all earlier attempts to calculate the fluid
volume in the tissue. It suddenly becomes clear that it is possible to
obtain the basic dependences between the parameters defining it, without
the necessity of any practical measurement. In the substituting diagram
of the capillary it is sufficient just to write any random values of R
and C in order to obtain the type of the dependence sought. This
gives enormous relief to the adherents of practical measurements in
physiology, because the results of every experiment can be predicted.
Then the actual experiment is conducted, if that is necessary at all,
merely to confirm or visualize the theoretical formulation of the
problem under consideration.}

_{Here we shall
describe some of the corollaries of the new microcirculation theory:}

_1. _{The most important corollary is
undoubtedly the finding that the value of the effective hydraulic
pressure EFP in the intact tissue is not reduced with the value of COP,
as was believed so far. This conclusion, as well as a necessary
correction of the earlier values of the capillary filtration coefficient
CFC (Petrow, 1990e), face physiologists with the fact that the
filtration in the human capillary network for one day is perhaps 100-200
times more than the norm of about 20 litres accepted now. This means the
need of radical changes in the existing physiology concepts.}

_2. _{The advantage which Nature creates
for itself by introducing the COP factor consists in the fact that a
considerably more intensive tissue perfusion is possible with COP than
without COP. Here we are referring to the paracapillary flux through the
interstitium, which brings oxygen and vitally necessary substances to
the cells, and takes the slag back to the blood and out of the body.
Without COP, the same flux through the interstitium would occur with a
much higher tensile strength than with COP. With respect to the blood
pressure, COP reduces the swelling of the tissue and its sheath 1:1,
making it more compact and more viable.}

_3. _{The application of the new theory to
explain the function of the lungs is of particular interest. (1) The
lungs can function correctly only if the COP values exceed those of the
blood pressure. Under normal conditions, the fluid film in the lung
alveoli closes the interstitium of the respiratory capillaries from the
side of the air. Here the surface tension of the alveolar fluid acts as
a thin membrane, which is completely sufficient for preventing the
penetration of air bubbles in the blood. (2) Subatmospheric hydraulic
pressure exists in this specific type of "interstitium", which
keeps the lungs "dry" and makes respiration possible. (3)
Under the effect of the blood pressure, a paracapillary convective flux
passes in this interstitium, assisting the function of the lungs. This
flux assists the saturation of the blood with oxygen and the elimination
of slags, poisons, bacteria and other harmful additives, which penetrate
there from the air.}

_4. _{The condition for prevalence of COP
over the blood pressure should also be fulfilled in the soft tissues,
e.g., in the subcutaneous tissue or in the tissue below the serous
mucosae in the body, otherwise they would develop an oedema and would
not be able to perform their functions. With the help of COP, a
subatmospheric (negative) hydraulic pressure with suction in the
direction of the capillaries is created. Nevertheless, the interstitium
of the soft tissues continues to be perfused by a paracapillary
convective flux, which is created by the blood pressure. This ingenious
invention of Nature is the reason for the close adhesion of the skin and
all kinds of mucous membranes to the body or to the internal organs. In
this way, the necessary conditions for body movements of the individual
are created and for the same reason fluids injected into the
subcutaneous tissue are rapidly resorbed.}

_5. _{The natural capillary contains an
infinite number of pores, and equilibrium between the filtration and
refiltration with respect to the interstitium is automatically
established on this capillary tubing. Life shows that this equilibrium
is maintained within the different types of physiological loading of the
organism. This means that the actual construction of the porous
capillary and the surrounding area creates the conditions for the
enormous stability of the tissue perfusion. On the other hand, COP gives
an opportunity for additional intensification of this perfusion.}

_{The
blood capillary and the area around it in the form of the
paracapillary cylinder represent a self-optimizing and a self-adapting
system, which guarantees stable and viable blood supplying to the
tissues.}

_{3.2.
Discussion 2: New interpretation of the isogravimetric method}

_{The
isogravimetric method was considered so far in physiology as the most
serious proof of Starling's hypothesis (Michel, 1997, p. 14):}

_{“The
experimental result of Pappenheimer & Soto-Rivera (1948) were a
complete vindication of Starling`s hypothesis that fluid across
microvascular walls are determined by differences in hydrostatic and
oncotic pressure."}

_{More
details in discussing the method of Pappenheimer and Soto-Rivera were
already presented in another paper about CFC (Petrow, 1990e), which will
be translated into English shortly. Of course, the antagonism between
the blood pressure and COP is a fact, because a rise in the blood
pressure increases the volume of the cell tissue, whereas a rise in COP
reduces this volume. However, this does not mean that blood pressure and
COP oppose each
other at
the level of the capillary wall. According to the new microcirculation
theory, the antagonism between the blood pressure and COP concerns not
the fluid flux through the capillary wall, but the interstitial
hydraulic pressure (IHP). Therefore, the essence of the gravimetric
method consists precisely in the presentation of a constant IHP value,
with a view to preserving the cell tissue volume also constant. When
this is known, the isogravimetric method can already be used not for
confirming, but - conversely - for rejecting Starling's hypothesis.}

_{For
instance, in the case when the values of the blood pressure and of COP
increase, but the difference between these two parameters remains
constant, e.g.: 20 - 16 = 40 - 36 = 60 - 56. In this case the convective
fluid exchange should remain constant, because the effective filtration
pressure, according to Starling's hypothesis, does not change in all
three cases. According to the new microcirculation theory, the
convective paracapillary flux through the interstitium will increase
considerably. Every researcher conducting experiments in this field will
confirm this conclusion, if he stains the interstitial fluid and
measures the rate of its elimination from the tissue for the different
values of the cited parameters. With the higher values of the blood
pressure and of COP, the staining substance is eliminated faster, and
this fact cannot be explained with Starling's hypothesis. Conversely, it
fits perfectly the new theory.}

_{The
rise in the blood pressure leads to increased tissue volume for two
reasons:}

_1. _{The elevated blood pressure
increases the difference between the averaged pressures in the
capillaries and in the interstitium. Consequently, a certain amount of
fluid will pass into the interstitium and will increase the interstitial
pressure IHP, and hence the tissue volume as well.}

_2. _{The elevated blood pressure expands
the blood vessels from the arterial side. This effect contributes to the
additional increase of the tissue volume.}

_{The
compensating rise in COP with the isogravimetric method reduces the
pressure in the interstitium and hence the tissue volume. However, COP
does not influence the volume of the additionally expanded blood vessels.
Therefore, the isogravimetric points will occur in this case at a higher
COP value than can be expected under the simplified theoretical model,
see a real
theoretical model by Petrow (1990e).}

_{The
isogravimetric curve from bottom to top, i.e., from low blood pressure
to high blood pressure, will shift to the right for the cited reason,
whereas conversely, top to bottom, it will shift to the left for
analogous reasons. The hysteresis effect obtained confirms the new
theory. It is specific for each type of tissue and is influenced by the
properties of the interstitium and of the blood vessels in it. The
isogravimetric method can be used in practice for determining these
properties, which is important for making the theoretical tissue model
more concrete.}

_{3.3.
Discussion 3. The errors in Starling's hypothesis and in the current
microcirculation theory}

_{Starling
discovered 100 years ago that most of the fluid filtered in the tissue
interstitium partially returns to the capillaries, which was a
considerable achievement for his time. Even if it had been only for that
achievement, Starling would have remained for us a great researcher,
whom we would always respect.}

_{However,
to make an assumption that, for instance, in Starling's quotation in
Section 2.1, or to derive a dependence of the type of equation (1), does
not mean in the least that this can happen as an isolated act in itself
in a theory. In reality, both the verbal expression and the mathematical
formula involve above all an obligation to also define the conditions of
the theoretical model for which they are valid (compare with Fig. 2).
For the same reason, a practical experiment cannot be an aim in itself,
it will only be wasted power if it is not supported 100% by a serious
theoretical concept. In all other cases it would have errors.}

_{For
example, if a spaceship is sent to Mars, it cannot be claimed that its
trajectory was partially correct, because that spaceship finally landed
on the Moon. Therefore, "slightly correct" ideas do not exist,
they are either correct or incorrect. This rule is universally valid,
because every idea can be fragmented ad infinitum into sub-ideas,
for which this "yes or no" type of assessment can always be
applied.}

_{Unfortunately,
no one has thought so far about the extent to which the model devised by
Starling is applicable in practice, and whether it can secure an
effective supply to the cell in tissues. For this reason, quite a number
of fallacies have accumulated in physiology for the past 100 years and
we shall examine them below:}

_1. _{Starling's idea that COP in the
intact tissue may stop fluid filtration is erroneous. Antagonism between
blood pressure and COP does exist, not at the level of the capillary
wall, as Starling believed, but at the level of the interstitial
hydraulic pressure IHP. In this way, the blood pressure increases IHP,
whereas COP reduces it, making IHP the most important factor that can
oppose the blood pressure, in order to obtain a sensible equilibrium of
the forces in the tissue (action=reaction). The static pressure in the
blood vessels is also completely neutralized by IHP, see item 21 below.}

_2. _{This situation also solves the
energy problem about which we wrote in Section 1. With the new
microcirculation theory, COP does not create energy losses against the
blood pressure, because the antagonism between these two parameters is
transferred to the level of the interstitium. It is normal to expect
such a result of Nature, because it not only does not tolerate empty
spaces, but it likewise does not tolerate solutions that are not
optimal.}

_3. _{Starling's assumption that the COP
factor causes fluid resorption from the interstitium (cf. Starling's
quotation in 2.1) is also erroneous, because essentially refiltration
and not resorption exists in the intact tissue. We are introducing here
the concept of "refiltration" in order to distance ourselves
from Starling's "resorption", which he uses not at the place
where it actually exists (see item 7 below).}

_4. _{We divide the convective flux in the
interstitium on the capillaries into "filtration" in the
direction of the interstitium and "refiltration" back to the
capillaries. The motive force of this flux is the difference in the
blood pressure from the beginning to the end of the capillaries, and the
phenomenon follows Ohm's Law, see Fig. 3b1 and Fig. 7. The division into
"filtration and refiltration" is purely formal and it is done
to differentiate between the part of the flux that enters the
interstitium and the other part that leaves it. In a steady state, the
filtration and refiltration are "automatically" equalized.}

_5. _{The lymph in the tissue is not formed
as a residue of the fluid filtered in the interstitium, as was believed
until now. The lymph is actually the result of the accumulation of
osmotically active substances in the interstitium, Petrow (1990b, 1991).}

_6. _{Even in the case of the transient
processes, such as the sudden rise in COP, an additional part of the
interstitial fluid will return to the capillaries, not because it will
be resorbed: (1) The rise in COP immediately provokes a decrease in the
interstitial pressure (see Figs. 6f and 6g). (2) Because of this, the
elastic parameters of the interstitium become unloaded, they shrink and
in this way they refilter a part of the interstitial fluid back to the
capillaries.}

_7. _{A real resorption occurs, for
example, when COP in the blood suddenly increases in the case of tissue
oedema. However, this is already a pathological situation, which cannot
be valid for the intact tissue as well. This is why, we insist on
determining correctly the concepts of resorption and refiltration.
Incidentally, Starling conducted his experiments mainly on oedematous
tissues, which may be the reason for his erroneous conclusions.}

_8. _{The concept of "refiltration"
was not alien to Starling and he defined it in his paper (Starling,
1896) as "back filtration". However, Starling firmly rejects
this possibility, assuming that the higher interstitial pressure would
cause the venules to collapse, see also C.C. Michel, p. 10. Here we are
referring to another of Starling's assumptions, which is also wrong.
Theory has shown that the capillaries will not collapse under similar
conditions, but will pulsate rhythmically. Elsewhere we have even given
an experimental setup that demonstrates this in practice (Petrow, 1991).
The blood flow during these pulsations of the venules cannot be
interrupted.}

_9. _{The meaning of the new theoretical
setup will be understood even by non-specialists, because only now it
has become possible to determine correctly the role of COP in the blood.
It is known now that the convective flux through the interstitium occurs
under all circumstances. However high the resultant COP may be, it
cannot prevent the nutrient flux to the cells, if the tissue intactness
is preserved. The new theory demonstrates above all an optimum supply of
the cells with high stability of the blood supply process of the tissue.
These conclusions cannot be obtained either with Starling's formulation,
or with the more recent studies, which actually only develop further
Starling's ideas.}

_10. _{Equation
(1) and the graph on Fig. 1 do not express the interaction of the
parameters in the intact tissue, as physiologists still believe.
Actually, they refer to a pathological situation in which the lungs are
simply filled with water. However, even in that case equation (1) cannot
be used for calculating the process. A massive lung oedema, of the type
that occurs after drowning, is calculated according to the new theory
and in compliance with Fig. 5.}

_11. _{The
capillaries are structures with distributed parameters. If equation (1)
is used to calculate them, then these complex structures would be
reduced to one pore or to a ring of pores (see Fig. 3a). It is more
important, however, that there is no rule in mathematics that would
allow us to do that.}

_12. _{Precisely
in terms of the criticism in item 10, researchers of microcirculation
have persistently sought for decades a value of IHP, which they can
substitute in equation (1). During that time all kinds of practical
methods were proposed for its measurement, which will not be discussed
here.}

_13. _{The
living organism consists of most varied tissues. It is self-evident that
each tissue has is specific IHP. Moreover, it is quite logical to assume
that this IHP from the external wall of a porous capillary wall changes
according to some law and that it has not one, but an uninterrupted
series of values. Similarly, the blood pressure inside and along the
same capillary wall changes constantly and declines progressively. Any
other assumption would be erroneous.}

_14. _{Therefore,
it would be totally pointless to seek any methods for IHP measurement:
(1) because no practical method can be so precise as to measure the real
IHP values; (2) moreover, even the best IHP measurements bring no
benefit, if the experimenter does not know how to interpret them.}

_15. _{We
believe that no suitable method for IHP measurement will be found in the
future, either. On the other hand, IHP can be easily calculated if some
angular parameters are known, e.g. the blood pressure in the beginning
and at the end of the capillaries, the COP profile, the permeability of
the capillary wall, the elastic properties of the interstitium, etc.
Unlike IHP, these parameters can be really measured.}

_16. _{There
is not one single reason that would give us evidence to assume that the
hydraulic pressure would remain constant in the interstitium on the
outer side of a capillary, if at the same time on the inside of that
capillary the blood pressure or COP change. "Due to the incredible
difficulties in the IHP measurement, we were forced so far to assume IHP
to be a constant value in the in vivo experiments"- Pappenfuß,
1993. Unfortunately, such excuses are not accepted in mathematics and it
is likewise not acceptable to draw convenient conclusions just because a
value allegedly cannot be measured. It is also impossible to measure
directly the distance to the Sun with a ruler. However, this is no
obstacle for proposing a sensible model for its calculation. It is
perfectly natural to introduce simplifications in science, but they have
to be very well grounded in order to lead through induction to more
general conclusions. The condition IHP = const. cannot be substantiated
in the microcirculation theory.}

_17. _{It
is not possible to substantiate the property of the infinite capacity of
the interstitium. This property, however, is directly required, if the
condition IHP = const. is to be accepted. No one can substantiate the
claim that the capillaries are actually in an infinitely large
compartment filled with fluid, or that the interstitium is simply open.
Therefore, IHP = const. cannot be merely an ordinary assumption.
According to mathematics, IHP = const. is above all an obligation for
certain properties of the interstitium.}

_18. _{In
practical experiments it is observed that the intact tissue starts
diminishing its volume, if COP increases suddenly. This process stops
after a short time and this ostensibly simple fact is the best proof
that IHP cannot be a constant value, because there is practically no
other force in the tissue, which can neutralize the influence of the
suddenly increased COP. Here only the response decrease in IHP is in a
position to stop the additional fluid flux to the capillaries and thus
to stop the volume reduction of the tissue. At IHP = const., this
process would be terminated only if the COP value is diluted by the
hypotonic interstitial influx to the initial level. The effect of COP
dilution can easily be compensated by a specially designed experimental
setup.}

_19. _{IHP
= const. in the space behind a permeable wall as that of the capillary
requires an interstitium with an infinite capacity to accumulate water.
Such an interstitium would have to be open, but there are no such cases
in living Nature on land. Here even the lungs present a closed
interstitium, which is located between at least two permeable walls in
the tissue space from the air to the blood. At the same time, it also
prevents air embolism in the blood and achieves in this way one of the
most important phenomena of life creation: the respiration by the lungs
(for details see 3.1.).}

_20. _{In
the case of pulmonary oedema, the interstitium suddenly becomes open (see
Fig. 5). The capillaries in fish gills should also have an open
interstitium: in the future it would therefore be necessary to focus
attention on the mechanisms for regulating the fluid exchange there. In
a practical experiment, the capillary interstitium can be open
unnaturally, e.g., by destroying the capillary cylinder. In practice,
these are the few examples in the animal world, when it is possible to
talk about open interstitium.}

_21. _{A component of the blood pressure
acts in the lower limbs of a standing human being, which may exceed
several times the COP value. This is the static pressure and it can be
compensated only by a response increase in IHP. There is no other force
in the tissue to compensate this pressure and to stand behind the
permeable capillaries. Its value shows that the strength of the
interstitial bonds, especially in case of the muscle interstitium,
should be sufficient strong to withstand this loading. They also show
that it would simply not be serious to try to speak here about an open
interstitium. Cave: Soft tissues are not able to
compensate static pressures.}

_22. _{Every scientist-physiologist should
pose the question how the cell tissue would be fed, if there were}_{truth
that a prevalence of COP over the blood pressure would stop the
convective flux around the cells. The assumption about the alleged
prevalence of the diffusion in that case cannot be substantiated,
because the real diffusion is very slow to overcome the relatively large
spaces between the capillaries in such a short time. This simple fact
has been ignored in physiology until now. Moreover,
in semi-permeable membranes like the capillaries and when there is a
concentration gradient, the diffusion is always connected with fluid
convection in the tissue, Petrow (1991). At
the same time, it seems to be difficult to understand that most
processes around the capillary wall are easily explained with the
well-known classical laws of hydraulics (see Fig. 7).}

_{The
contribution of the present paper consists in the application of a new
method for calculating the fluid exchange processes around the capillary
wall. The new theoretical formulation yields results, which are above
all accurate, logical and sensible. Moreover, for the first time it is
possible to demonstrate a concept that appeared to be optimal and to
work precisely in the way which
is to be expected a priori in living Nature.}

_{The new
approach to these problems also shows us that there are other omissions
and errors in physiology, which merit most detailed investigation in the
future. They refer to problems as: (1) Capillary filtration coefficient,
CFC, Petrow (1990e); (2) Edema and formation of lymph, Petrow (1990b);
(3) The role of the blood pulsation and blood amplitude, Petrow (1990c)
(4) The movement of the colloids through capillary membranes, Petrow
(1990d, 1991, and 1992).}

_{No
assumptions have been made in the new theory, so that there is no one
reason to call it a
hypothesis. The new theory is simply mathematics, therefore it is as
true as mathematics can be true generally. The use of the new theory for
calculating capillary processes is both convenient and expedient. From a
scientific and logical point of view, the new theory is mandatory for
solving problems of the type of fluid exchange on the capillary wall.}

_{A
more detailed version of this theory can be found in German on the
Internet: http:\\www.petrow.de}

_Figures:

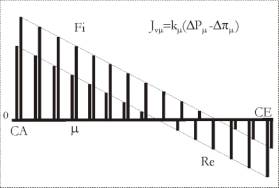
_{Fig.
1: Profile of the fluxes Jvm
through the capillary wall along the capillary in accordance with
Starling's hypothesis. The insignificant increase in the blood pressure
leads to critical prevalence of the filtration (see the second series of
values). If such a construction of the tissue perfusion is to function
(to become real), the interstitium around the capillaries should be open.
D}_P_{m
and D}_p_{m
are respectively the hydraulic pressure and the oncotic pressure
differences flanking the capillary membrane. km
presents a dimension coefficient, and CA and CE mark respectively the
capillary entrance and the
capillary end.}

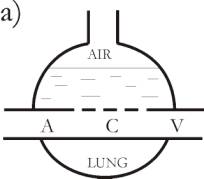
_{Fig.
2: Three different possibilities for cell tissue construction. On Fig.
2a1 the interstitium above the capillary wall is open (this is valid of
column 1) and here the interstitial hydraulic pressure IHP is constant,
being determined by the height of the water column. Fig. 2 a2 shows a
soft tissue, e.g., the subcutaneous tissue (this is valid of column 2),
in a state of oedema, and Fig. 2a3 presents schematically a cell tissue,
which should possess sufficient internal bindings so as to withstand the
loading by Pc, e.g. the muscle tissue (this is valid of column
3). A, C and V designate the arterial, capillary and venous part of the
blood vessels. Pc and}_p_{d
are respectively the mean pressure in the capillaries and the oncotic
pressure difference upon the capillary wall; I = interstitial space.}

_{Fig.
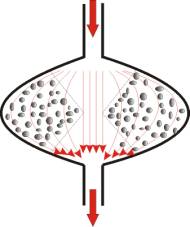
3: Sometimes the dimensions of the capillary or the way of its
incorporation in the surrounding tissues allows it to be considered as
an element with only one pore or with a ring of pores. In that case, COP
and the blood pressure act opposite each other and the influence of COP
cannot be compensated, although the interstitium is closed (Figs. 3a1
and 3 a2).}

_{It can be seen
from Figs. 3b1, 3b2, 3b3 and 3b4 that the compensation of COP may occur
only with capillaries, which may be presented as elements with at least
two or more (Fig. 3a3) pores, or with at least two or more rings of
pores, respectively. The liquid medium in the interstitium is the link
along the chain, so that, for instance, the suction force of COP at the
end of the capillary to be transmitted with the opposite sign to the
suction force of COP in the beginning of the capillary, Fig. 3b3. In
this way, the forces of COP, acting along the capillary, mutually reduce
each other to zero (Fig. 3b4).}

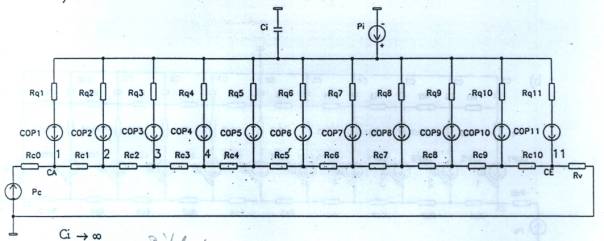
_{Fig.
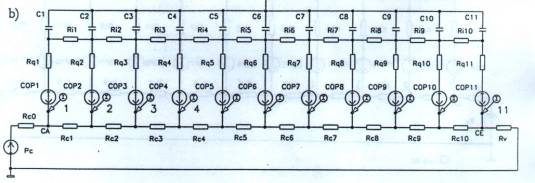
4. 4a: Describing of a capillary segment with elementary length D}_l_{and the elementary values Cm}_,_{Ri, Rq, Rc and}_p_{dm.
The set of numerous such segments forms the summary substituting
configuration, which is shown on Fig. 4b with 11 capillary segments. Rc0
and Rv are here the resistances of the blood vessels before and
after the capillary. In Fig. 4b the resultant value of the oncotic
pressure pd
is designated with the initials COP. PCA and PCE are
respectively the blood pressure at the entrance and the blood pressure
at the end of the capillary.}

_{Fig.
5. 5a: The pathological situation of lungs filled with water corresponds
quite correctly to Starling's hypothesis and can be used for
demonstration purposes. 5b: The substituting capillary configuration of
pulmonary oedema in accordance with Fig.5a and Figs. 4a and 4b. 5c:
Distribution of the transcapillary flux along the capillary at a
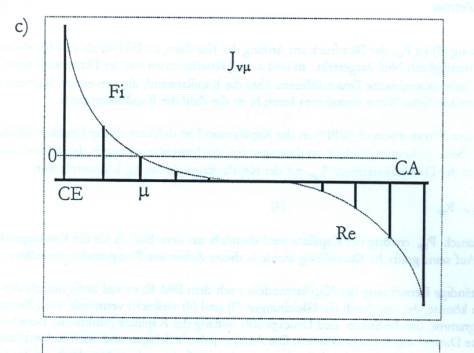
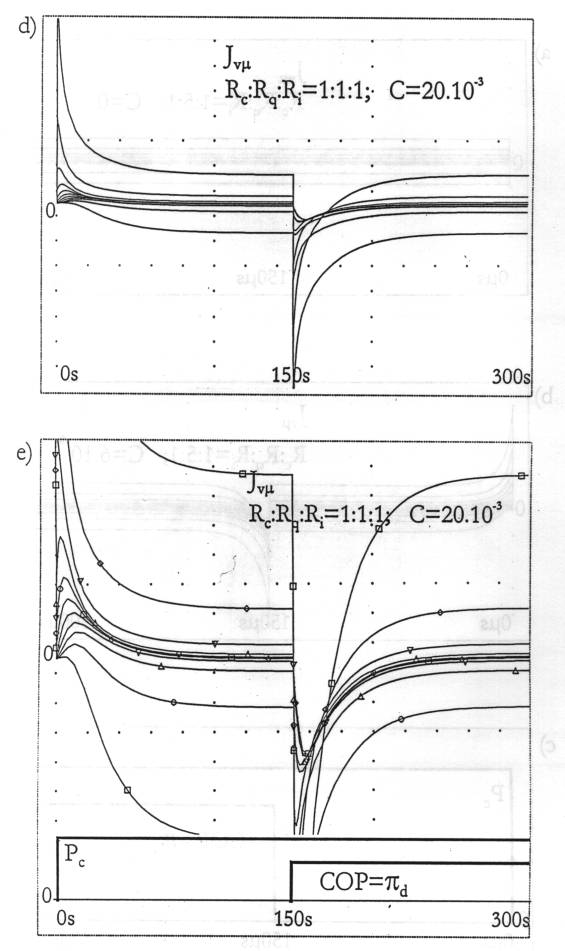
definite moment in time t = 150s (cf. Fig. 5d). It is interesting to
note that the base line in Fig. 5c shifts downwards under the influence
of the constant IHP. 5d: Dependence of the transcapillary flux on time
for different values of the blood pressure Pc and the oncotic
pressure difference}_p_{d,
designated here with COP, see Fig. 5e.}

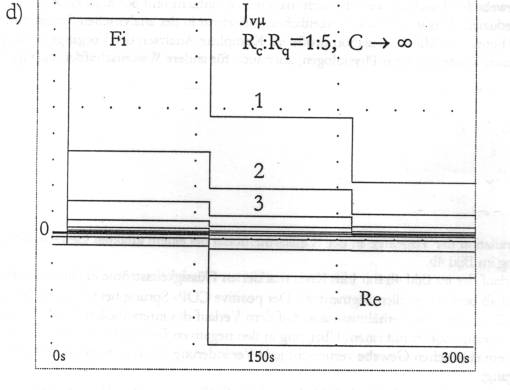
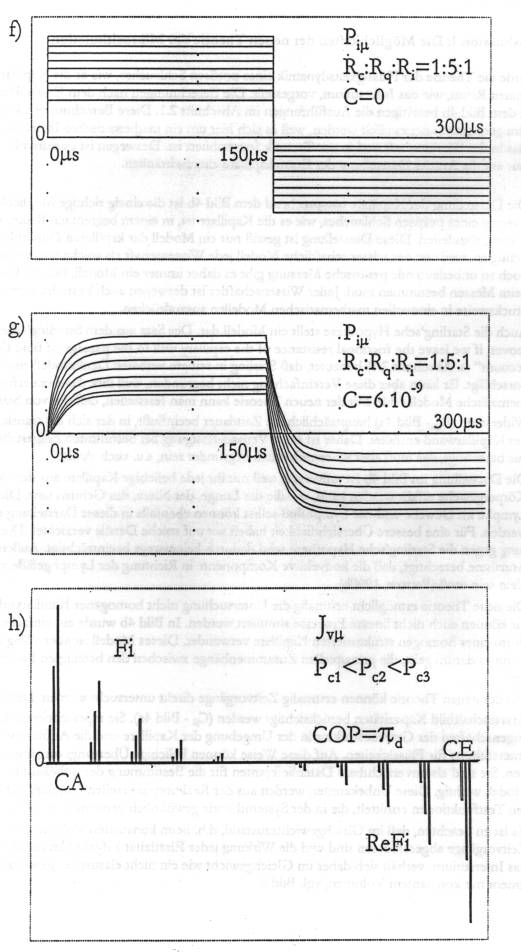
_{Fig. 6:
Simulation of the capillary fluid exchange for intact tissue according
to the substituting configuration on Fig. 4b. 6a: Dependence of the
transcapillary flux on time for tissues with a non-elastic interstitium
- on Fig. 4b for Ci= 0 in all segments. The positive leap of COP
at 150ms has no
influence on the processes of filtration and refiltration. On the other
hand, the interstitial hydraulic pressure IHP (Fig. 6f) makes a
momentary leap in the negative area. 6b: In the tissue with elastic
interstitium, each leap in the blood pressure or in COP generates a
transient process with a definite duration. 6c: Graphic image of the
blood pressure in the beginning of the capillary and of COP for all
capillary segments. 6d: Considerable changes in the tissue elasticity Cm and in the
values of the resistances Ri : Rq : Rc do not
induce qualitative changes in the type of the transient process (cf.
Fig. 6b). 6e: Detailed image of the graphs on Fig. 6d around the zero
line. 6f: Change in the interstitial hydraulic pressure IHP in a tissue
with a non- elastic, and in Fig. 6g - with elastic interstitial space,
respectively. 6h: In the intact tissue the ratio between filtration and
refiltration is preserved and the system remains stable even after a
manifold rise in the blood pressure.}

_{Fig.
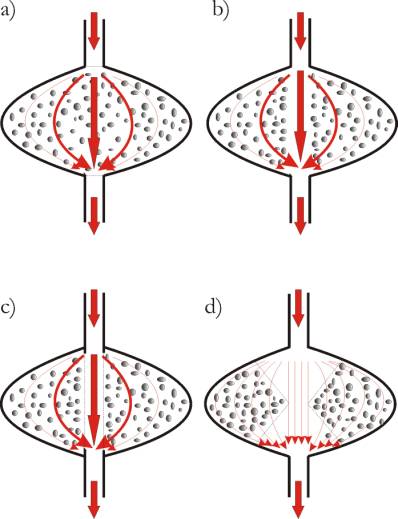
7: The blood supply to the tissue with the help of capillaries is
normally a pressure-perfusion transversely across the tissue. Moreover,
the interstitial flux is distributed according to Ohm's Law in the same
way as the small balls placed in a suitable bag are washed by a water
jet (Fig. 7a). Here the water pressure regulates the speed of the
washing and the system remains stable until the bag in which the balls
are placed bursts. With more prolonged washing, the small balls which
obstruct the strongest jet line will be pressed to the sides, forming a
channel in the middle, as shown on Fig. 7b. The principle of this
washing will not change, if a water-permeable membrane is gradually
formed on the inner surface of this channel (Fig. 7c). In this way,
Ohm's Law as a fundamental principle in hydraulics and the channeling
effect of hydraulic pressure are the most important mechanisms
facilitating the formation of new capillaries in the traumatized and
oedematous tissue after injury. 7d: Stylized presentation of the tissue
to visualize the action of Ohm's Law: the areas at a greater distance to
the capillary wall are less perfused, because they exercise a higher
hydraulic resistance to the fluid flux.}

_{4.
References:}

_{Landis,
E.M. (1927)}_.

_{Micro-injektion
studies of capillary permeability II. The relation between capillary
pressure and the rate at which fluid passes through the walls of single
capillaries. American Journal of Physiology 82, 217-238.}

_{Michel,
C.C. (1997).}

_{Starling:
The Formulation of his Hypothesis of microvascular fluid exchange and
its significance after 100 Years. Experimental Physiology (1997), 82,
1-30.}

_{Papenfuß,
H.-D. (1993).}

_{Gutachten
zur Habilitationsschrift des Dr.med. Dr. Ing. Jordan M. Petrow mit dem
Titel: Theorie der Mikrozirkulation im Gewebe und ihre praktische
Anwendung. Unveröff.
Manuskript, Archiv
der Universität Rostock.}

_{Pappenheimer,
J.R., A. Soto-Rivera (1948).}

_{Effective
osmotic pressure of the
plasma proteins and other quantities associated with the capillary
circulation in the hindlimbs of cats and dogs. Am. J. physiol. 152,
471-491.}

_{Petrow,
J.M. (1990a).}

_{Theorie
der Mikrozirkulation, Teil 1: Die Fehlinterpretationen in der Starling’schen
Hypothese der Mikrozirkulation. Z . gesamte
inn. Med. 45, H18, 531-535.}

_{Petrow,
J.M. (1990b).}

_{Theorie
der Mikrozirkulation, Teil 2: Die Probleme der Mikrozirkulation aus der
Sicht der neuen theoretischen Konzeption.
Z . gesamte inn.
Med. 45, H18, 535-540.}

_{Petrow,
J.M. (1990c).}

_{Theorie
der M,ikrozirkulation, Teil 3. Die
Rolle der Blutdruckamplitude bei der Mikrozirkulation im Gewebe.
Z.gesamte inn. Med. 45 H21, 633-638.}

_{Petrow,
J.M. (1990d).}

_{Theorie
der, Mikrozirkulation, Teil 4: Die Bewegung von Molekülen durch
semipermeable Membranen. Z.
gesamte inn. Med. 45 H23,
695-703.}

_{Petrow,
J.M. (1990e).}

_{Neue
Methode zur Bestimmung des kapillären Filtrationskoeffizienten im
Gewebe. Teil 1 und Teil 2. Z. gesamte inn. Med. 45
H5, 137-144.}

_{Petrow,
J.M. (1991).}

_{Theorie
der Mikrozirkulation und ihre praktische Anwendung.
Teil 1-3. Habilitationsschrift, Unveröff. Manuskript, Archiv der
Universität Rostock.}

_{Petrow,
J.M. (1992).}

_{Kritik
an der Anwendung des Reflexionskoeffizienten s
nach Stavermann in der Theorie der Mikrozirkulation. Z. gesamte inn.
Med. 47 H2, 78-82.}

_{Starling,
E.H. (1896).}

_{On the
absorbtion of fluids from connective tissue spaces. Journal of
Physiology 19,
312-326.}